Confidence Interval

Confidence interval

[2021-01-08]

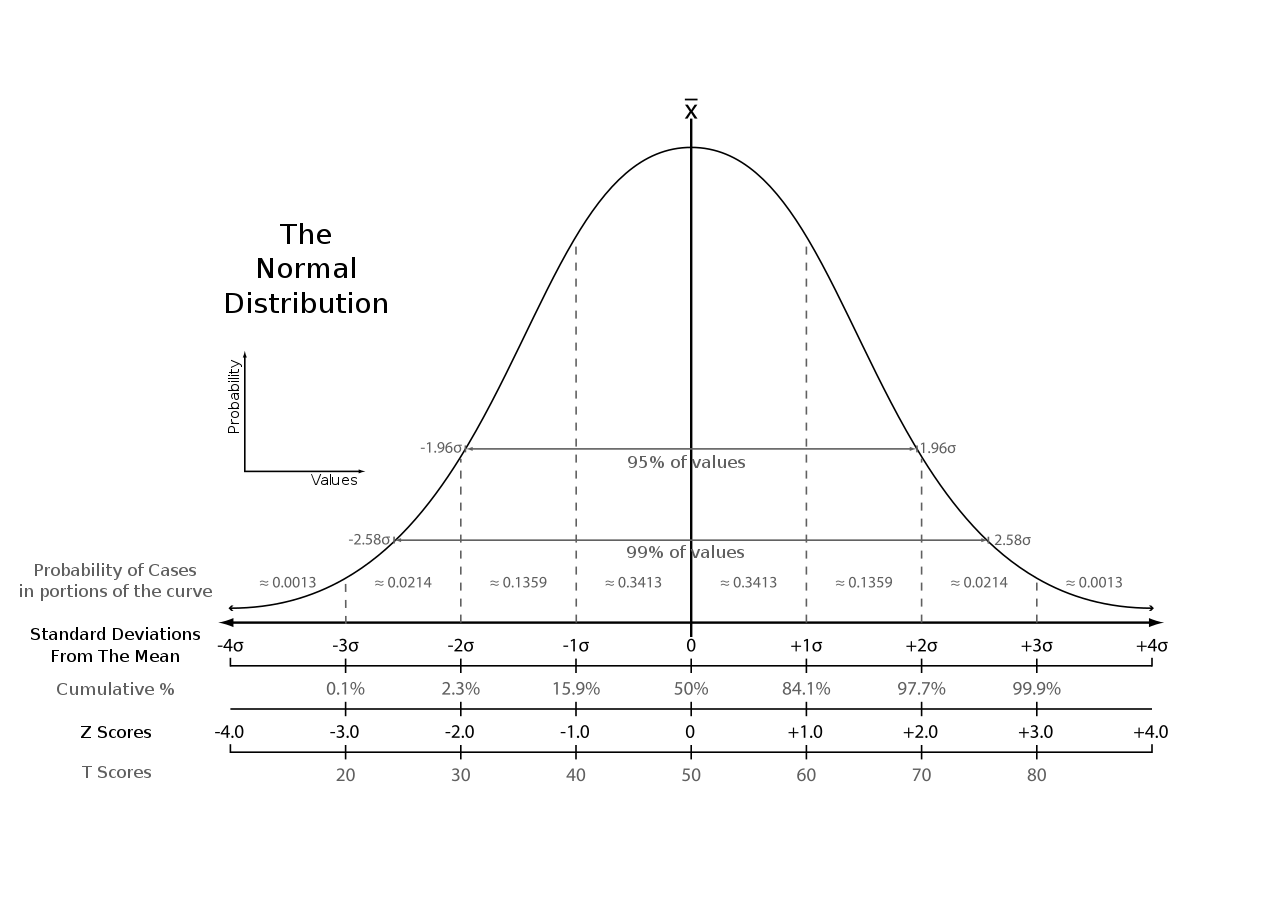
Confidence interval = ± z * standard deviation(x), where z is the number of standard deviations from the mean of the standard normal distribution we need to be to get a specific two-tailed significance level (e.g. for 95% significance this means ±1.96 standard deviations away from the mean, and ±2.58 standard deviations for 99% significance).

A 95% confidence interval is NOT interpreted as, there is 95% chance that the true mean lies within this interval.

A 95% confidence interval is an estimate specific to the experiment performed. If the experiment were to be repeated, a different confidence interval is likely to be estimated.

What 95% confidence interval mean is that, if we were to repeat the experiment multiple times, we expect that 95% of the confidence intervals we estimated independently from each experiment will contain the true mean.

It’s not the specific confidence interval which has the 95% chance of containing the true mean; but the collection of multiple confidence intervals estimated from multiple independent experiments.