Survival Analysis: Kaplan Meier Estimation Vs Logistic Regression

Survival analysis: Kaplan-Meier estimation vs logistic regression

[2021-06-01]

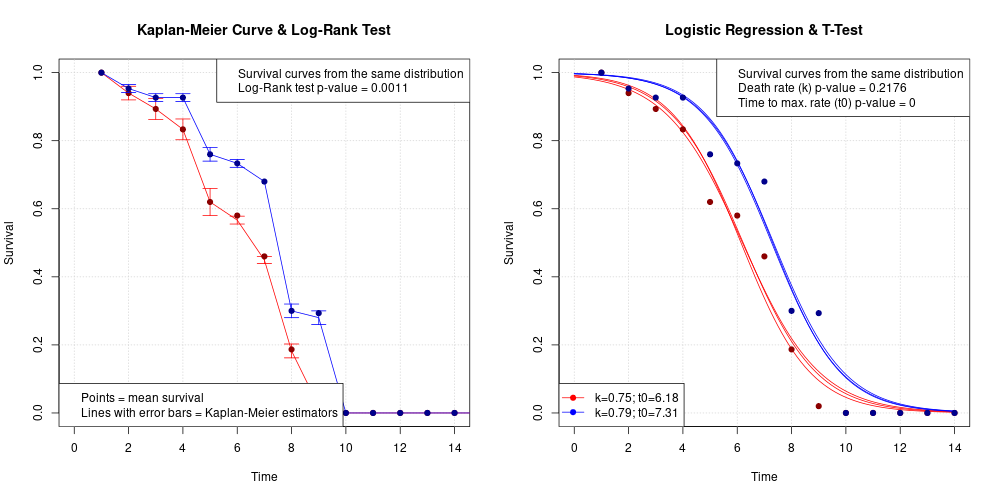
Kaplan-Meier estimation and logistic regression allow tests of statistical significance between various survival (or growth) datasets. Logistic regression allows us to ask more precise questions about the statistical significance of these differences than Kaplan-Meier estimation.

Kaplan-Meier estimation is non-parametric, while logistic regression is parametric. This means that the Kaplan-Meier estimation does not assume that the observed survival data we wish to model as a function of time follows a probability distribution like the normal or Gaussian distribution, Piosson distribution and bionomial distribution. On the other hand, logistic regression assumes that the observed survival data follows the logistic distribution.

Kaplan-Meier survival function estimation

The Kaplan-Meier estimator, also known as the product limit estimator of the survival function \(f(t)\) at time \(t\) is defined as:

\[\hat f(t) = \prod_{i|t_i<t} \left ( 1 - {d_i \over n_i} \right )\]

where \(t_i\) is the \(i^{th}\) time before \(t\) where at least 1 death occurred, \(d_i\) is the number of deaths that occurred at time \(t_i\) (\(d_i \ge 1\)), and \(n_i\) is the number of individuals which are still surviving at time \(t_i\).

To test whether or not two survival functions modelled using the Kaplan-Meier estimators are significantly different, the log-rank test is usually performed.

Logistic regression

The logistic function can be defined as:

\[y = y_{min} + \left ( { y_{max}-y_{min} \over 1 + e^{-k(t-t_0)} } \right )\]

where \(y\) is the survival (or growth) data, \(y_{min}\) and \(y_{max}\) are the minimum and maximum survival, respectively which can be set as constants or parameters to be estimated, \(k\) is the maximum survival rate per unit time \(t\), and \(t_0\) is the time at which \(k\) occurs. These parameters are estimated using various cost function minimisation algorithms.

The estimated logistic function parameters which best fit the data (e.g. \(\hat y_{min}\), \(\hat y_{max}\), \(\hat k\), and \(\hat t_{0}\)) are used to compare the different datasets. T-tests on each parameter can be used to test for significant differences.

Statistical significance tests

For Kaplan-Meier estimation, the log-rank test will yield a p-value which answers whether or not the two survival (or growth) data are significantly different.

For logistic regression, the parametric nature of this method allows us to ask more specific questions, e.g. which survival (or growth) data has a lower \(y_{max}\), higher \(y_{min}\), higher maximum rate (\(k\)), and which one lags behind in terms of \(t_0\).

Illustration

############################################################################################
### Simulate data by sampling from a Poisson distribution (with lamdba==day) for 14 days ###
############################################################################################
set.seed(2318008) ### culture
### initialise the vectors of the number of individuals in the two datasets (vec_N1, and vec_N2), time (vec_t), and the number of replications (r)
vec_N1 = c(50)
vec_N2 = c(50)
vec_t = 0:14
r = 3
### sample the number of individuals dying from a Poission distribution
for (t in tail(vec_t,-1)){
    d1 = rpois(n=1, lambda=t)
    d2 = rpois(n=1, lambda=t)
    N1 = max(c(0, tail(vec_N1,1)-d1)) ### limit to min(N)==0
    N2 = max(c(0, tail(vec_N2,1)-d2)) ### limit to min(N)==0
    vec_N1 = c(vec_N1, N1)
    vec_N2 = c(vec_N2, N2)
}
### simulate 3 replicates with normally distributed error
func_sim_reps = function(vec_N, r=3){
    mat_error = matrix(round(rnorm((length(vec_N)-1)*r, mean=0, sd=1)), nrow=r)
    mat_d = matrix(rep(diff(vec_N), times=r), byrow=TRUE, nrow=r) + mat_error
    mat_d[mat_d>0] = 0
    ### make sure that the zero differences reflect the changes made by the random error on the previous time-point
    idx_zeros = mat_d==0
    idx_val = cbind((mat_d==0)[,2:ncol(mat_d)], rep(FALSE,r))
    mat_d[idx_zeros] = mat_d[idx_val]
    ### put together the simulated replicated survival data
    mat_N = matrix(rep(vec_N, times=r), byrow=TRUE, nrow=r)
    mat_N[,2:ncol(mat_N)] = mat_N[,2:ncol(mat_N)] + mat_d
    mat_N[mat_N<0] = 0
    df_N = expand.grid(TIME=1:ncol(mat_N), REP=1:r)
    df_N$N = matrix(t(mat_N), byrow=FALSE, ncol=1)
    return(df_N)
}

###############################
### Kaplan-Meier estimation ###
###############################
func_KaplanMeier_estimators = function(df_N){
    df_N$D = NA
    df_N$F = NA
    for (rep in unique(df_N$REP)){
        vec_N = df_N$N[df_N$REP==rep]
        vec_D = abs(diff(vec_N))
        vec_f = c(1)
        for (t in 1:(length(vec_N)-1)){
            vec_n = vec_N[1:t]
            vec_d = vec_D[1:t]
            if (vec_d[t]==0){
                vec_f = c(vec_f, tail(vec_f,1))
            } else {
                f = prod(1 - (vec_d/vec_n))
                vec_f = c(vec_f, f)
            }
        }
        df_N$D[df_N$REP==rep] = c(0, vec_D)
        df_N$F[df_N$REP==rep] = vec_f
    }

    ### not sure if this is the right thing to do: just average the Kaplan-Meier estimators per time-point
    vec_mu_N = aggregate(N~TIME, data=df_N, FUN=mean)
    vec_sd_N = aggregate(N~TIME, data=df_N, FUN=sd)
    vec_mu_D = aggregate(D~TIME, data=df_N, FUN=mean)
    vec_sd_D = aggregate(D~TIME, data=df_N, FUN=sd)
    vec_mu_F = aggregate(F~TIME, data=df_N, FUN=mean)
    vec_sd_F = aggregate(F~TIME, data=df_N, FUN=sd)
    
    df_KM = data.frame(TIME=vec_mu_N[,1], N=vec_mu_N[,2], D=vec_mu_D[,2], F=vec_mu_F[,2], sd_N=vec_sd_N[,2], sd_D=vec_sd_D[,2], sd_F=vec_sd_F[,2])
    return(df_KM)
}

#######################################################################
### Log-Rank Test for the Kaplan-Meier-estimated survival functions ###
#######################################################################
func_logRank_test = function(df1, df2){
    vec_N1 = head(df1$N,-1); vec_D1 = tail(df1$D,-1)
    vec_N2 = head(df2$N,-1); vec_D2 = tail(df2$D,-1)
    vec_N = vec_N1 + vec_N2
    vec_O = vec_D1 + vec_D2
    vec_E1 = vec_N1 * (vec_O/vec_N)
    vec_E2 = vec_N2 * (vec_O/vec_N)
    vec_V1 = vec_E1 * ((vec_N-vec_O)/vec_N) * ((vec_N-vec_N1)/(vec_N - 1))
    vec_V2 = vec_E2 * ((vec_N-vec_O)/vec_N) * ((vec_N-vec_N2)/(vec_N - 1))
    z = sum(vec_D1 - vec_E1, na.rm=TRUE) / sqrt(sum(vec_V1, na.rm=TRUE)) ### also z = sum(vec_D2 - vec_E2, na.rm=TRUE) / sqrt(sum(vec_V2, na.rm=TRUE))
    pval = 2*pnorm(q=abs(z), mean=0, sd=1, lower.tail=FALSE) ### 2-tail
    return(pval)
}

#########################
### Logistic function ###
#########################
logistic_func = function(y_max, y_min, k, t0, t){
    y_min + ((y_max - y_min) / (1 + exp(k*(t-t0))))
}

######################################################################
### Cost function of the logistic function given the observed data ###
######################################################################
cost_func = function(par, y_max, data){
    y_min = par[1]
    k = par[2]
    t0 = par[3]
    t = data[,1]
    y = data[,2]
    y_pred = logistic_func(y_max=y_max, y_min=y_min, k=k, t0=t0, t=t)
    return(sum((y-y_pred)^2))
}

######################################################
### Estimation of the logistic function parameters ###
######################################################
func_logistic_regression = function(df_N){
    df_LR = data.frame(REP=unique(df_N$REP))
    df_LR$y_min = NA
    df_LR$k = NA
    df_LR$t0 = NA
    for (rep in unique(df_N$REP)){
        vec_t = df_N$TIME[df_N$REP==rep]
        vec_N = df_N$N[df_N$REP==rep]
        vec_y = vec_N/max(vec_N, na.rm=TRUE)
        optim_out = optim(par=c(1, 1e-4, 1),
                        fn=cost_func,
                        y_max = 1,
                        data=cbind(vec_t, vec_y),
                        method="L-BFGS-B",
                        lower=c(0, 1e-5, 0),
                        upper=c(1, 1, max(vec_t)))
        y_min = optim_out$par[1]
        k = optim_out$par[2]
        t0 = optim_out$par[3]
        df_LR$y_min[df_LR$REP==rep] = y_min
        df_LR$k[df_LR$REP==rep] = k
        df_LR$t0[df_LR$REP==rep] = t0
    }
    return(df_LR)
}

######################################################
### Simulate the 2 datasets with 3 replicates each ###
######################################################
df_N1 = func_sim_reps(vec_N=vec_N1, r=r)
df_N2 = func_sim_reps(vec_N=vec_N2, r=r)

#################################################
### Kaplan-Meier estimation and log-rank test ###
#################################################
df_KM1 = func_KaplanMeier_estimators(df_N=df_N1)
df_KM2 = func_KaplanMeier_estimators(df_N=df_N2)

### test 2 different curves but sampled from the same distribution
LOG_RANK_PVAL_SIMILAR_DIST = func_logRank_test(df1=df_KM1, df2=df_KM2)

### test the same curve
LOG_RANK_PVAL_SAME_DIST = func_logRank_test(df1=df_KM1, df2=df_KM1)

########################################
### Logistic regresstion and t-tests ###
########################################
df_LR1 = func_logistic_regression(df_N=df_N1)
df_LR2 = func_logistic_regression(df_N=df_N2)

### test the k and t0 of the 2 curves sampled from the same distribution
LOGISTIC_PVAL_SIMILAR_DIST_k = t.test(x=df_LR1$k, y=df_LR2$k)$p.value
LOGISTIC_PVAL_SIMILAR_DIST_t0 = t.test(x=df_LR1$t0, y=df_LR2$t0)$p.value

### test the k and t0 of the same curve
LOGISTIC_PVAL_SAME_DIST_k = t.test(x=df_LR1$k, y=df_LR1$k)$p.value
LOGISTIC_PVAL_SAME_DIST_t0 = t.test(x=df_LR1$t0, y=df_LR1$t0)$p.value

############
### Plot ###
############
par(mfrow=c(1,2))

### Plot Kaplan-Meier estimation results
plot(x=0, y=0, xlim=c(min(vec_t), max(vec_t)), ylim=c(0,1), main="Kaplan-Meier Curve & Log-Rank Test", xlab="Time", ylab="Survival", type="n"); grid()
lines(x=df_KM1$TIME, y=df_KM1$F, lty=1, col="red")
arrows(x0=df_KM1$TIME, x1=df_KM1$TIME, y0=(df_KM1$F-df_KM1$sd_F), y1=(df_KM1$F+df_KM1$sd_F), code=3, angle=90, length=0.1, col="red")
points(x=df_KM1$TIME, y=df_KM1$N/max(df_KM1$N), pch=19, col="darkred")
lines(x=df_KM2$TIME, y=df_KM2$F, lty=1, col="blue")
arrows(x0=df_KM2$TIME, x1=df_KM2$TIME, y0=(df_KM2$F-df_KM2$sd_F), y1=(df_KM2$F+df_KM2$sd_F), code=3, angle=90, length=0.1, col="blue")
points(x=df_KM2$TIME, y=df_KM2$N/max(df_KM2$N), pch=19, col="darkblue")
legend("topright", legend=c("Survival curves from the same distribution",
                            paste0("Log-Rank test p-value = ", round(LOG_RANK_PVAL_SIMILAR_DIST,4))))
legend("bottomleft", legend=c("Points = mean survival", "Lines with error bars = Kaplan-Meier estimators"))

### Plot logistic regression results
plot(x=0, y=0, xlim=c(min(vec_t), max(vec_t)), ylim=c(0,1), main="Logistic Regression & T-Test", xlab="Time", ylab="Survival", type="n"); grid()
mat_t_new = matrix(rep(seq(min(vec_t), max(vec_t), length=100), times=r), byrow=TRUE, nrow=r)

mat_y_new = logistic_func(y_max=1, y_min=df_LR1$y_min, k=df_LR1$k, t0=df_LR1$t0, t=mat_t_new)
for (i in 1:nrow(mat_y_new)){
    lines(x=mat_t_new[1,], y=mat_y_new[i,], col="red")
}
points(x=df_KM1$TIME, y=df_KM1$N/max(df_KM1$N), pch=19, col="darkred")

mat_y_new = logistic_func(y_max=1, y_min=df_LR2$y_min, k=df_LR2$k, t0=df_LR2$t0, t=mat_t_new)
for (i in 1:nrow(mat_y_new)){
    lines(x=mat_t_new[1,], y=mat_y_new[i,], col="blue")
}
points(x=df_KM2$TIME, y=df_KM2$N/max(df_KM2$N), pch=19, col="darkblue")

legend("topright", legend=c("Survival curves from the same distribution",
                            paste0("Death rate (k) p-value = ", round(LOGISTIC_PVAL_SIMILAR_DIST_k,4)), 
                            paste0("Time to max. rate (t0) p-value = ", round(LOGISTIC_PVAL_SIMILAR_DIST_t0,4))))
legend("bottomleft", legend=c(paste0("k=", round(mean(df_LR1$k),2), "; t0=", round(mean(df_LR1$t0),2)),
                              paste0("k=", round(mean(df_LR2$k),2), "; t0=", round(mean(df_LR2$t0),2))), lty=1, pch=19, col=c("red", "blue"))